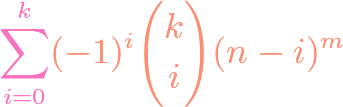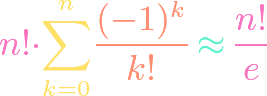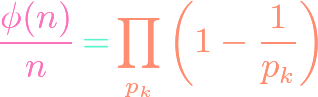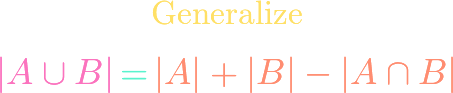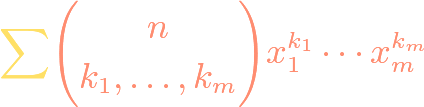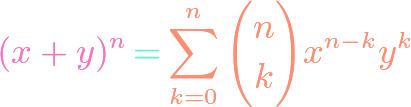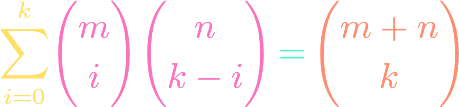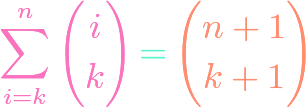https://www.youtube.com/watch?v=ZXIsCe3EZKE Given two finite sets, we might wonder how many surjections exist that map from one to the other. It turns out that this question, and a generalization, can be answered using the principle of inclusion-exclusion (PIE). Moreover, if the output codomain has more elements than the input domain, then the number of surjections is …
https://www.youtube.com/watch?v=NkFbv1jxcdE Derangements are permutations with no fixed points, meaning no element gets mapped to itself. We use the principle of inclusion-exclusion to derive as simple as possible a formula for the number of derangements of a given finite set. Amazingly, it turns out that, as the number of elements goes to infinity, the fraction of …
https://www.youtube.com/watch?v=Kl9WH5Eev2o Euler’s totient formula tells us the number of positive integers less than or equal to a given positive integer that are relatively prime to the latter. This is an important function in combinatorics and number theory. The function can be computed in a fairly simple fashion if we know the list of distinct prime …
https://www.youtube.com/watch?v=fl2eoGBIT70 Given two finite sets, we can find the cardinality of their union by adding the two individual cardinalities and subtracting the cardinality of the intersection. But how can we find the cardinality of the union of $n$ finite sets? This is the general principle of inclusion-exclusion, otherwise known as PIE. We state this general …
https://www.youtube.com/watch?v=2UHlMA-Qcg0 The multinomial theorem generalizies the binomial theorem by replacing the power of the sum of two variables with the power of the sum of an arbitrary finite number of variables $$(x_1+x_2+cdots+x_m)^n.$$ This is the result that gives rise to the concept of multinomial coefficients.
https://www.youtube.com/watch?v=5n8qXRTVUps In the binomial theorem, the goal is to expand the polynomial expression $(x+y)^n$ and find the coefficients after like terms have been collected. This is a very useful result in mathematics as a whole, and it is particularly useful in combinatorics for proving combinatorial identities.
https://www.youtube.com/watch?v=-yLJ8G_i_vM If we have $m$ cats and $n$ dogs, in how many ways can we choose $k$ of the animals? By iterating through the possible combinations of dogs and cats, we can derive a combinatorial identity, which is called Vandermonde’s identity. We derive this identity here using the described combinatorial or committee-forming proof.
https://www.youtube.com/watch?v=hk98kUxk-V0 The hockey stick identity in combinatorics tells us that if we take the sum of the entries of a diagonal in Pascal’s triangle, then the answer will be another entry in Pascal’s triangle that forms a hockey stick shape with the diagonal. Although proofs by induction or Pascal’s identity are possible, we show a …
https://www.youtube.com/watch?v=jAcbcWV9CyE Similar to the question of summing a row of Pascal’s triangle, we can consider summing the squares of the entires of a row of Pascal’s triangle. By a combinatorial argument involving cats and dogs, we show that $$binom{n}{0}^2+binom{n}{1}^2+cdots+binom{n}{n}^2=binom{2n}{n}.$$
https://www.youtube.com/watch?v=1Ovnz74AasA If one takes the sum of a row of entries in Pascal’s triangle, one finds that $$binom{n}{0}+binom{n}{1}+cdots+binom{n}{n}=2^n.$$ In this video, we prove this remarkable combinatorial identity in two ways: by forming a committee and substituting numbers into the binomial theorem.