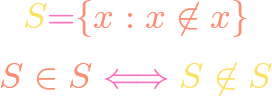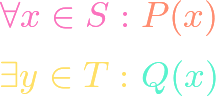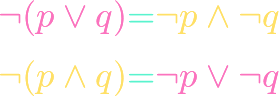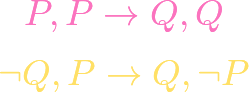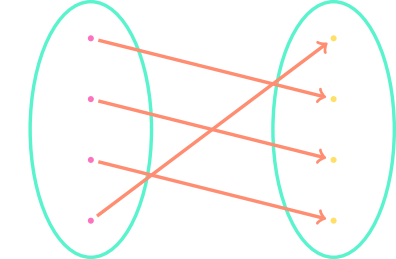
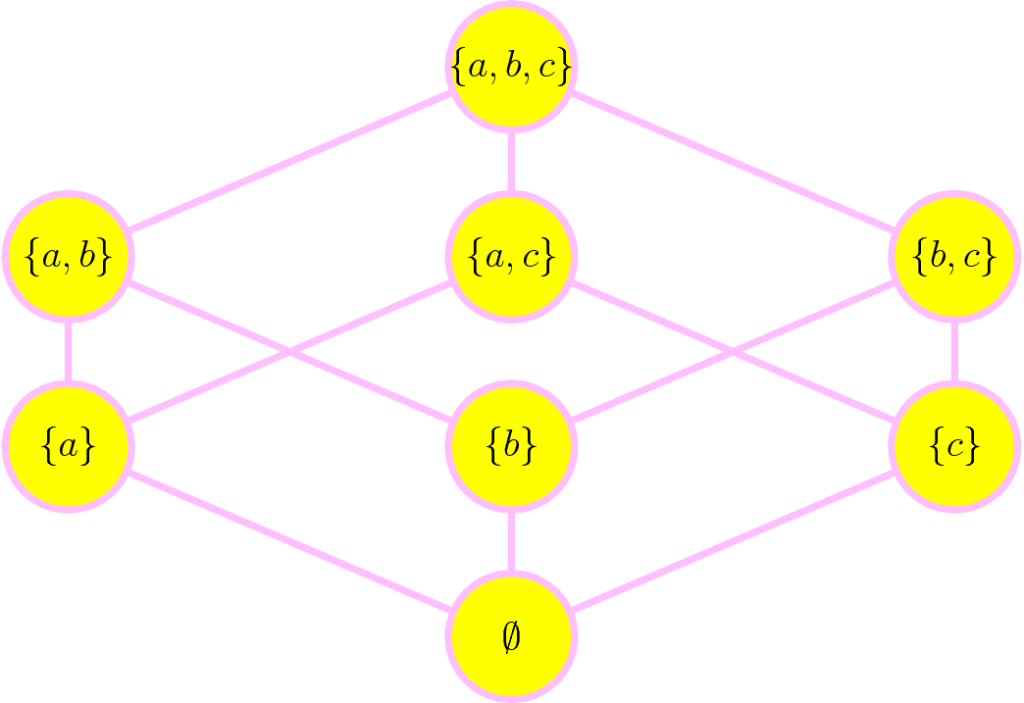
https://www.youtube.com/watch?v=oTXvwc3k8ag Cantor’s paradox derives a contradiction from the assumption that there is a set of all sets. Like Russell’s paradox, this proves that there can be no set whose elements are all sets; in other words, the mathematical universe is not a set. The main tool is Cantor’s theorem, a topic on which we have …
https://www.youtube.com/watch?v=7FQu540d3-A By repeatedly taking the power set $mathcal{P}(S)$ of an infinite set $S$, Cantor’s theorem shows that these new infinities get strictly “bigger and bigger.” So there exists an infinite hierarchy of infinities in the sense that the lower infinities cannot map surjectively onto the higher infinities (but injective maps are possible).
http://www.youtube.com/watch?v=ZeJZFaP6dL8 A function $f: X to Y$ is bijective (both injective and surjective) if and only if it has an inverse $f^{-1} : Yto X$ (a function that is both a left-inverse and a right-inverse). We prove this biconditional result here.
https://www.youtube.com/watch?v=Drsqa4XFgJQ Bertrand Russell’s paradox in set theory shook the foundations of the mathematical world in 1901 by showing that naive set theory leads to a contradiction. This caused mathematicians to adopt the convention that one cannot summon elements directly from the entire mathematical universe into a set, and that there is no set of all …
https://www.youtube.com/watch?v=cCEvHZgq188 One of the most powerful and general concepts in math is the idea of a partial order. We show that, given that we are working within a universl set, its subsets fall into a partial order under the subset relation $Xsubseteq Y$. This means that the subset relation is reflexive, antisymmetric, and transitive.
https://www.youtube.com/watch?v=LJjJbljEOVs Logical quantifiers are often bounded like $forall xin S: P(x)$. That is, we say that universally or existentially quantified elements satisfy a predicate (like being a member of some set) before stating the condition to be fulfilled. We describe such logical sentences here.
https://www.youtube.com/watch?v=DOu1kjAXutU Learn to negate logical expressions involving disjunctions and conjunctions using De Morgan’s laws $$neg(pvee q) equiv neg p wedge neg q,$$ and $$neg(pwedge q) equiv neg p vee neg q.$$
https://www.youtube.com/watch?v=xXaFCq0eesc Ever wonder what happens if something is both true and false, that is $Pwedge neg P$? For mathematicians, it is a doomsday scenario because it causes everything else to be both true and false as well. This is called the principle of explosion.
https://www.youtube.com/watch?v=PR0bBAZUlG4 We discuss why the classic logical arguments of modus ponens $$P,Prightarrow Q, Q$$ and modus tollens $$neg Q, Prightarrow Q,neg P$$ are valid forms of argument.