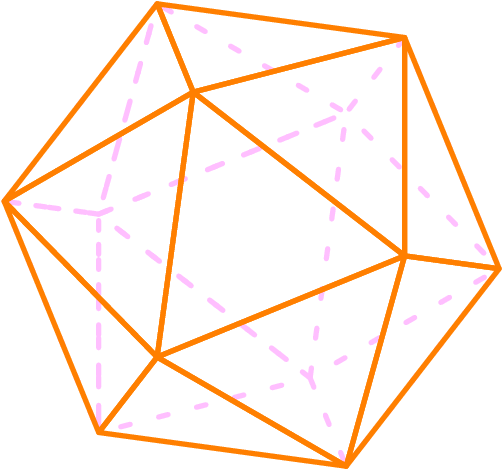
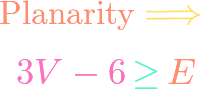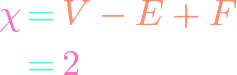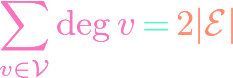Binet’s Formula for Fibonacci Numbers
https://www.youtube.com/watch?v=bgjQDilbHE8 The Fibonacci numbers are among the most prolific of number sequences, perhaps second only to the Catalan numbers. They can be defined recursively, but one may ask if there exists a closed formula for the sequence. This is answered by Binet’s formula, which takes on a form so strange that it is hard to […]
Binet’s Formula for Fibonacci Numbers Read More »