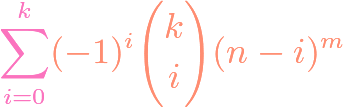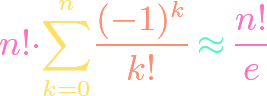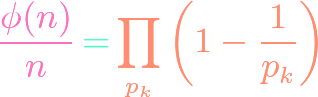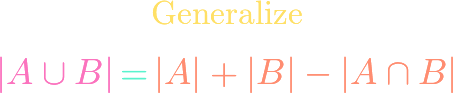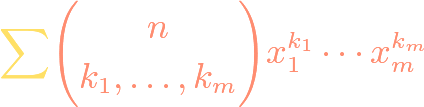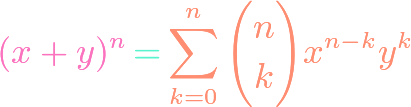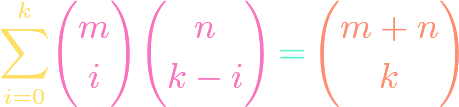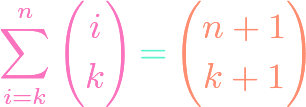Counting Surjections in Combinatorics
https://www.youtube.com/watch?v=ZXIsCe3EZKE Given two finite sets, we might wonder how many surjections exist that map from one to the other. It turns out that this question, and a generalization, can be answered using the principle of inclusion-exclusion (PIE). Moreover, if the output codomain has more elements than the input domain, then the number of surjections is […]
Counting Surjections in Combinatorics Read More »