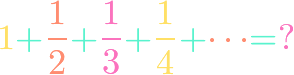Fractions of the form $frac{1}{n}$ go to zero as $n$ goes to infinity, but what if we add them all up? A surprising classic result is that this sum can get arbitrarily large. We prove the divergence of the harmonic series here.

https://www.youtube.com/watch?v=Of0LRRMoO78 The change of base identity for logarithms is a highly useful technique for dealing with logarithm problems. We prove this identity $$log_b x = frac{log_c x}{log_c b}$$ and then use it to derive a few other identities as corollaries.

When we have square roots in the denominator of a fraction, it can be desirable to transform the fraction into the same number but with a different presentation where the denominator is rational. We show a method for achieving this goal, with the main technique being the difference of squares factorization $$a^2 – b^2 =

https://www.youtube.com/watch?v=RRcRDVCA7Bg Even functions $f$ are symmetric across the $y$-axis, meaning $f(-x)=f(x)$. Odd functions $g$ are symmetric across the origin, meaning $g(-x)=-g(x)$. As long as the domain of a function is symmetric across $0$ on the real line, it turns out that the function can be uniquely written as a sum of an even function and

Adding a number to its negative produces $0$. Multiplying a non-zero number by its reciprocal produces $1$. We show that, given a fixed element that has an inverse in an associative binary operation (like addition or multiplication), the inverse is unique. So a number cannot have more than one negative or more than one reciprocal.

Given a binary operation, an identity element is like $0$ for addition or $1$ for multiplication: operating on a different number with it does not change that number. We show that, if an identity element exists, it is unique. So there cannot be two identity elements.