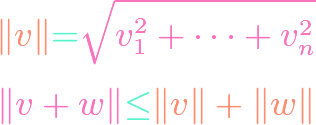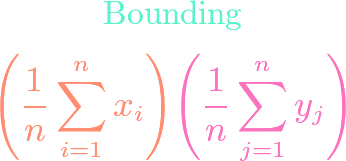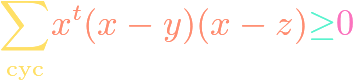https://www.youtube.com/watch?v=aZLZWJZ4cdQ In math, there are various triangle inequalities, ranging from the classical one that actually applies to triangles to one for the complex numbers. In this video, we derive the triangle inequality related to the Euclidean norm and inner product for tuples of real numbers.
https://www.youtube.com/watch?v=f8N4biffzhw We prove Chebyshev’s inequality for two number sequences using several applications of the rearrangement inequality. The goal is to make upper and lower bounds on the expression shown in the thumbnail. These inequalities come in handy on math contests and olympiads.
https://www.youtube.com/watch?v=hcK1MoIVbTA In math contest and olympiad circles, Schur’s inequality is known as a result which has special cases that are equivalent to relatively strong results. We prove the ordinary version of Schur’s inequality in this video. Stronger versions have been unearthed in recent years, such as by Valentin Vornicu.
https://www.youtube.com/watch?v=Oe4Qn_T69-I The real number Cauchy-Schwarz inequality is a multivariable inequality that holds for all real inputs. It has a variety of special cases, including the famous Engel’s form, that have found popular use on math contests and olympiads. Outside of contests, it is useful on optimization problems and in linear algebra. Here, we present an …
https://www.youtube.com/watch?v=iNldQpfT_ug The arithmetic mean – geometric mean inequailty is a famous multivariable inequality that allows us to compare the sum of some non-negative numbers with their product, in the presence of some other operations. This amazing multivariable inequality has widespread use across mathematics, including on math contests and olympiads. This proof is even more remarkable, …
https://www.youtube.com/watch?v=v4YVOMJAuGQ The Sophie Germain identity is a remarkable polynomial factorization. It is frequently useful in math contests, competitions, and olympiads. One would not expect this polynomial to factor, but an ingenious trick via the difference of squares factorization allows for the factorization $$x^4+4y^4 = (x^2-2xy+2y^2)(x^2+2xy+y^2).$$
https://www.youtube.com/watch?v=5zMtEQhFzvM&t We derive and describe the factorizations for a difference $a^n-b^n$ or sum $a^n+b^n$ of two same powers. In particular, this generalizes the famous and useful difference of squares factorization $$a^2-b^2=(a-b)(a+b).$$
https://www.youtube.com/watch?v=ssnPaJjNX-E Vieta’s formulas express the symmetric sums of the roots of the polynomial in terms of the coefficients of the polynomial. We derive these useful formulas and show how to write them in a compact form.
https://www.youtube.com/watch?v=z-M8o7WDALc The remainder and factor theorems for polynomials relate linear factors of a polynomial to its roots by utilizing properties of the Euclidean division of polynomials. Learn about these two important theorems by watching our video.
https://www.youtube.com/watch?v=RKNS4YjY6cU If a polynomial has real coefficients, then it turns out that the complex conjugate $a-bi$ of any of its complex roots $a+bi$ is also a root of the polynomial. We prove this amazing result here.