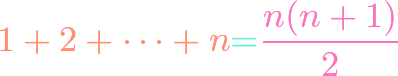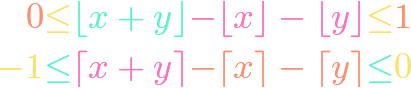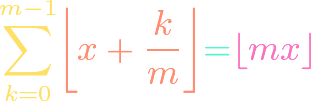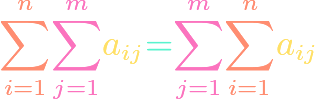Algebra

https://www.youtube.com/watch?v=wqHFq1OqmD4 Where an arithmetic series adds a common difference to each successive term, a geometric series multiplies successive terms by a common ratio. We show how to evaluate such a series, both in its finite and infinite variants. The infinite variant is one of the simplest infinite series that actually converge, and its formula is […]

https://www.youtube.com/watch?v=qrYlQc0j1Ao At a young age, Gauss shocked his teacher by finding the sum of the first $100$ positive integers quickly using the formula $$1+2+cdots+n=frac{n(n+1)}{2}.$$ We use a generalization of his techique to find the sum of an arithmetic series.

https://www.youtube.com/watch?v=EEI6ucn5FS8 We show the analogue of the triangle inequality when floor and ceiling functions replace absolute value. This results in some interesting inequalities that are useful in obtaining approximation results. The floor function one is $$0le lfloor x+y rfloor -lfloor x rfloor – lfloor y rfloor le 1.$$

https://www.youtube.com/watch?v=sBD3fp0XLT0 Hermite’s identity is a remarkable identity that allows us to simplify certain sums where each term involves the floor function. It comes up in math contests and olympiads from time to time. We prove this identity using an unexpected technique, namely periodicity.

https://www.youtube.com/watch?v=PEQ1-tjlnmo The reverse triangle inequality $$|x-y|ge ||x|-|y||$$ is a classic textbook exercise using the ordinary triangle inequality, but it is also a useful result in calculus or mathematical analysis. We prove it here using two different methods.

https://www.youtube.com/watch?v=mUhBemtfivQ The triangle inequality $$|x|+|y|ge |x+y|$$ for real numbers is an indispensable tool in mathematical analysis, otherwise known as calculus, because it allows us to approximate quantities by bounds. We prove a general version of it using the ordinary absolute value and for any number of variables.

https://www.youtube.com/watch?v=aLbfdbiAkXg Common knowledge says that banks give us a better deal by using compound interest instead of simple interest. Even though there are forces working in both directions, this is indeed true. This fact is equivalent to Bernoulli’s inequality. We also show that the AM-GM inequality can be used to prove that compounding more times

https://www.youtube.com/watch?v=yFPiHQ9fpkA Bernoulli’s inequality is a classic multivariable inequality $$(1+x)^m ge 1+mx$$ that allows us to compare an exponential expression with a linear one. Check out a proof by induction in this video.

https://www.youtube.com/watch?v=4pdI7xBIseM Are the integers bounded above by a real number? Nope. It turns out that for every real number, there exists an integer that exceeds it. We prove this property, called the Archimedean property, using a semi-secret but crucial property of the real numbers called Dedekind completeness.

https://www.youtube.com/watch?v=t_sZk0G_5w4 Sums and products can be written compactly using $sum$ and $prod$ notation, but it is sometimes possible to write the same sum or product in more than one way. The so-called discrete Fubini’s principle is a powerful method of exchanging the order in which the indices occur in a nested sum or product. It