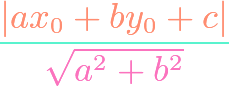https://www.youtube.com/watch?v=No1RIKHlxG4 Ceva’s theorem tells us when three cevians emanating from the three vertices of a triangle are concurrent. This is a handy theorem in math contests, competitions and olympiads. Its proof via proportional areas is quite interesting too since it uses a nice property of ratios that is unknown to many students.

https://www.youtube.com/watch?v=r-w9Jfls7YQ Pitot’s theorem gives us a nice fact about the side lengths of tangential quadrilaterals: the sum of one pair of opposite sides is equal to the sum of the other pair of opposite sides. We prove this result using a standard fact about tangents. There is a fallacious proof of the converse making its

https://www.youtube.com/watch?v=i6zPOQnQFRc There are several standard ways of identifying quadrilaterals that are cyclic. We investigate two such criteria using angles that are equivalent to cyclicity and prove their equivalence to the original definition. These criteria from Euclidean geometry are highly useful on math contests, competitions, and olympiads.

https://www.youtube.com/watch?v=NhrPI7utUrQ The power of a point theorem is a useful result in Euclidean geometry about lengths. Without proof, we present the theorem in a couple of ways and mention the various cases that come up in practice. This theorem is very useful on math competitions and olympiads.

https://www.youtube.com/watch?v=IJ6juhG1aE0 The inscribed angle theorem is an amazing fact of Euclidean geometry, which states that an inscribed angle has half the measure of the corresponding central angle. This leads to numerous other facts of angle geometry, including those about intercepted arcs and classifying cyclic quadrilaterals. We present a novel proof of the inscribed angle theorem

https://www.youtube.com/watch?v=QH8uy5CrFAo In the previous video, we proved Thales’ theorem which is about showing that a certain angle in a circle is right. We can go in the other direction and ask whether the vertex of the right angle lies on the circle. We address this important converse here and expose an ingenious proof of it

https://www.youtube.com/watch?v=HkG1RD4O-II Thales’s theorem in a basic yet important theorem in geometry. It tells us that if a triangle is inscribed in a circle such that one of the sides is a diameter, then the angle opposide the diameter is right. This remarkable property often comes in handy these days in math competitions, contests, and olympiads.

The law of cosines $$c^2=a^2+b^2-2abcdotcos C$$ is a generalization of the famed Pythagorean theorem to triangles that are not necessarily right. This formula is exceedingly useful in geometry, including in high school math and on math contests and olympiads. In our video, we prove the cosine law using geometric transformations.

https://www.youtube.com/watch?v=h8bbl609vBI There is a formula which tells us the perpendicular distance between a point and a line given in standard form. Though a more natural proof exists using vectors, we derive the formula in an elementary fasion in this video. The formula is an indispensable tool in Cartesian or coordinate geometry.

https://www.youtube.com/watch?v=C4yq-GSNO6k Many students know the double angle trigonometric identities, but what about triple angles? We derive the triple angle identities here using the addition and double angle identities.