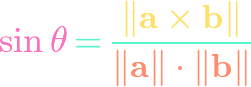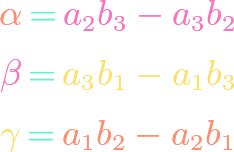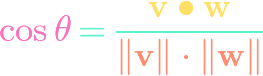https://www.youtube.com/watch?v=IwYHmNDHWtE Using the vector cross product formula and combining it with the trigonometric dot product, we find that we can express the sine of the non-reflex angle between two vectors in terms of the cross product. Another way of thinking about it is that the magnitude of the cross product is related to the sine …
https://www.youtube.com/watch?v=gpO4eW0kP_k Students in their senior high school year often learn the formula for the cross product of two three-dimensional vectors by heart. In this video, we derive the cross product formula from first principles and show an amazing way of remembering it using the determinant of a formal matrix.
https://www.youtube.com/watch?v=8iWPQKzqYII The dot product is a natural function that can be defined on a pair of Euclidean vectors. Interestingly, it can be combined with the cosine law to provide insight into the angle (or that angle’s explementary angle) between two vectors. Thus, we can derive what can be called the trigonometric form of the dot …
https://www.youtube.com/watch?v=8O8zwFx6mJI After the regular tetrahedron, the regular octahedron is the next simplest of the Platonic solids. In fact, the octahedron can be constructed by gluing together two square-based pyramids on their square faces. In this video, we present and prove simple formulas for calculating the surface area and volume of a regular octahedron in terms …
https://www.youtube.com/watch?v=RYX9HKDpQaU The regular tetrahedon is the simplest of the Platonic solids, otherwise known as regular polyhedra. In this video, show how to find the surface area and volume of a regular tetrahedron in terms of its edge length. The formulas $$V=frac{s^3}{6sqrt{2}} text{ and } S = sqrt{3} s^2$$ are surprisingly simple!
https://www.youtube.com/watch?v=XuGjYBiDdrQ The Pythagorean theorem tells us how to compute the length of the hypotenuse of a right triangle in terms of its legs. The 3-dimensional analogue of this problem is to determine the distance between two opposite corners of a rectangular prism. Such a line segment is called a space diagonal and we show that …
https://www.youtube.com/watch?v=D0mpQGdjoDw Almost everyone knows that the area of a triangle is base times height divided by 2. But there are numerous other ways of finding the area of a triangle. For example, if we are given only the three sides, we could use Heron’s formula. In this video, we show Heron, along with methods involving …
https://www.youtube.com/watch?v=NZ59VVsuEoM The law of sines is well-known, but its proof is not. It turns out that the expressions in the law of sines can be proven to all be equal to twice the circumradius, which not only proves the law of sines but extends it. We prove this result here, which says that $$frac{a}{sin A}=frac{b}{sin …
https://www.youtube.com/watch?v=0X5X6MwoMJQ Interestingly, it is possible to explicitly compute the lengths of the diagonals of any cyclic quadrilateral in terms of the side lengths of the cyclic quadrilateral. We derive these formulas here. This is not possible for arbitrary quadrilaterals.
https://www.youtube.com/watch?v=avmBOApiVSw Stewart’s theorem gives us an explicit formula for the length of a triangle cevian in terms of the ratio in which it splits the opposite side and the side lengths of the triangle. It can be applied to find formulas for the lengths of well-known cevians such as medians and angle bisectors. We prove …