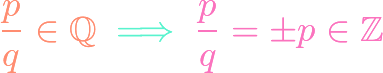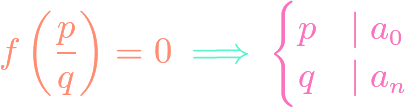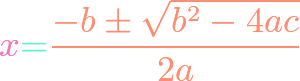Polynomial Integer Root Theorem
https://www.youtube.com/watch?v=fgBBJnhbMvI There are a couple of related theorems that we interchangeably call the “integer root theorem.” One tells us how to find that integer roots of a polynomial with integer coefficients. The second tells us that all rational roots of a monic polynomial with integer coefficients are integers. We prove both results in this video.
Polynomial Integer Root Theorem Read More »